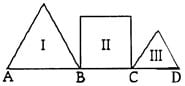
In this diagram, not drawn to scale, figures I and III are equilateral triangular regions with areas of 32√3 and 8√3 square inches, respectively. Figure II is a square region with area 32 square inches. Let the length of segment AD be decreased by 12.5% of itself, while the lengths of AB and CD remain unchanged. What’s the percent decrease in the area of the square?
- 12.5
- 25
- 50
- 75
- 87.5

The area of an equilateral triangle of side s is (s2√3)/4.
In I, (x2√3)/4 = 32√3 →x2/4 = 32 → x2 = 128 →
x = 8√2.
In II, y2 = 32 → y = 4√2.
In III, (z2√3)/4 = 8√3 → z2/4 = 8 → z2 = 32 → z = 4√2.
So AD = 8√2 + 4√2 + 4√2 = 16√2.
AD decreases by 12.5%, or 1/8, of itself, so it becomes 14√2. AB and CD are unchanged, so BC shrinks from 4√2 to 2√2.
The area of the square is now (2√2)2 = 8, down from 32, a loss of 75%.
The answer is (d).